by Edward T. Linacre

Geography Department,

School of Resource and Environmental Management

Australian National University, Canberra, Australia

Many weather stations include measurements of the evaporation from a US Class-A pan [1], as the basis for calculating the water loss from lakes or from crops [2, 3]. But most places are without such measurements, and, even where there is a pan, the measurements may be vitiated by poor maintenance, leading to errors due to leaks, the growth of algae in the water, an incorrect water level, weed-growth nearby, and so on. Also, it is hard to measure evaporation accurately during rainfall [4], perhaps because of splashing of water in or out of the pan. In view of these difficulties, it would be useful and cheaper to have some means of estimating pan evaporation with reasonable accuracy, from reliable climate measurements, such as temperatures [5]. Such estimates could provide values for places between those with reliable measurements, and facilitate a check on doubtful measurements.

The chief use of pan-evaporation data Ep lies in estimating lake evaporation Eo (or else the potential crop evaporation rate Et) by means of empirical factors. Parallel simultaneous measurements of Ep and Eo, for instance, yield the ‘pan coefficient’ Eo/Ep [6 - 8), and a knowledge of this factor, plus local pan measurements, give an estimate for Eo. Regrettably, the pan coefficient for a US Class A pan, for instance, has values widely scattered around 0.77, as shown by the eighteen papers listed in Appendix 1. It varies seasonally because of the lag of lake temperature [7] and increases linearly with the relative humidity, from 0.62 - 0.80 [9]. Such variability has caused this method of deriving Eo (or Et) to be replaced by direct estimation, preferably by means of the well-known equation of Penman [10].

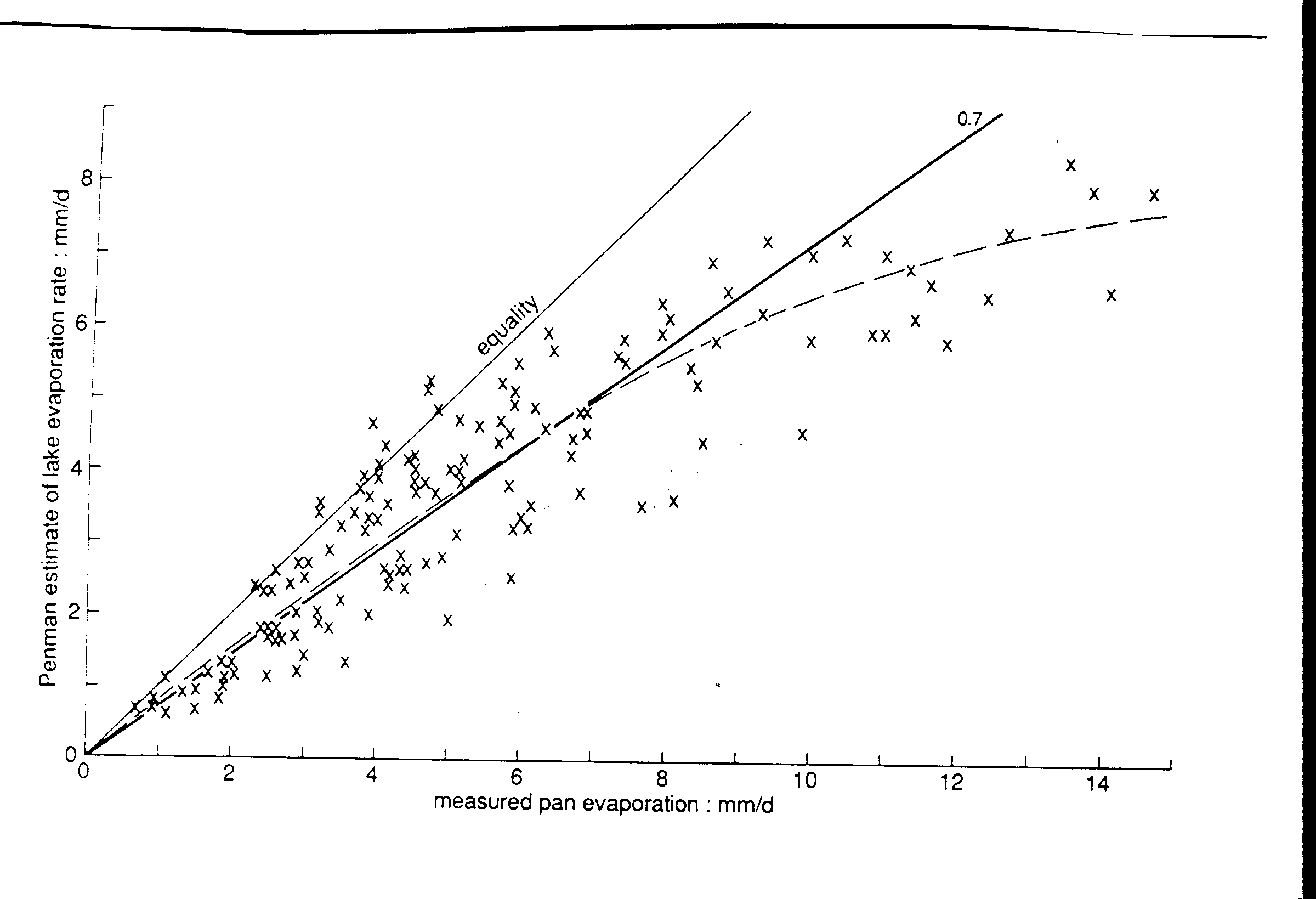
Measurements of pan evaporation Ep are compared with Penman estimates of lake evaporation EPen in Fig 1, from data in a review by Stanhill [11]. This shows twelve monthly-mean values from each of a dozen places around the world, indicating that EPen is less than Ep, especially at high evaporation rates. A rough figure for EPen/Ep is seen to be about 0.7, but the curvature of a line through the points demonstrates again that the ratio is not a constant. Also, the scatter of the points implies that no lake-evaporation formula based on Penman's original equation can be tested usefully by means of pan measurements.

Fig 1. Comparison of Penman estimates of monthly mean lake evaporation rates at twelve places, with US Class-A pan evaporimeter measurements there, using data given by Stanhill [11].

A disadvantage of the the Penman formula for Eo is that it requires measurements of temperature, humidity, wind and net irradiance, which are not all everywhere available. This was discussed in a previous paper [12], leading to the following simplified version -

where T is the average of the daily extreme Celsius temperatures, z the elevation (m), F allows for the change of air density with elevation and stands for [1.0 - 8.7 x 10-5 z], u is the wind speed (m.s-1) at 2 m, Td is the dewpoint temperature and Rs the solar irradiance of the lake's surface (W.m-2). The dewpoint can be estimated graphically from the daily extreme temperatures [13]. As regards Rs, two methods of estimating it were described earlier [12]. The more accurate method requires monthly rainfall data, as proxy for the cloud which cuts out some of the extra-terrestrial radiation, given in a table [14]. Often it is sufficient to estimate the wind speed approximately from measurements nearby or at other times, since evaporation varies much less than proportionally with changes of wind [3, 13]. Eqn 1 shows that the dependence on wind is least when radiation is strong. Consequently, only daily extreme temperature measurements are essential, with rainfall and wind speed data as desirable. Errors of estimating Eo with Eqn 1 were shown to be around 0.3 mm.d-1 at Copenhagen, for example.

Unfortunately, there are only a few reliable sets of lake-evaporation measurements for checking Eqn 1, whereas there are many measurements of pan evaporation Ep, from all over the world. So it is useful to modify the lake-evaporation equation to the case of a pan, to facilitate testing the universality of Eqn 1. That is the main purpose of the present paper.

Altering Eqn 1 to give the pan-evaporation rate Ep involves the geometry of the raised, circular pan, which affects its solar irradiance and advective heat transfer. The US Class-A pan is 1.21 m in diameter (so that the water surface has an area of 1.15 m2) with a wall 255 mm high (ie its outside area is 0.97 m2), and therefore the vertical section through a diameter has an area of 0.31 m2.

Sometimes the pan is screened by wire mesh to prevent birds and animals from drinking the water, especially in arid climates. This reduces the wind and radiation over the water's surface and consequently lowers the evaporation rate, depending on the size of the mesh. The reduction may be about 13% in a humid climate [15], or 10% in a semi-arid climate [16, 17].

The rate of pan evaporation depends on the input of energy, chiefly solar radiation. In addition to the solar radiation at the water surface of a pan, there is also a considerable transfer of heat through the wall, which affects the water’s temperature and hence its rate of evaporation. Insulating the wall and base reduces evaporation by as much as 29% [18]. Heat through the wall consists partly of radiation, and partly advection from the wind around. As regards the extra irradiance, there are four factors - a) exposure of the wall to direct sunshine, b) diffuse radiation from the sky onto the wall, c) solar radiation reflected onto the wall from the ground around, and d) longwave radiation from the surroundings. All this additional heating more than offsets the reduction of evaporation due to the albedo of a pan being about 14%, instead of 7% for water [13]. We will now consider the four factors.

a) The direct radiation in the total solar irradiance of the ground depends on the amount of cloud and on the Sun's elevation in the sky. When the Sun is at an angle Q above the horizon, it ‘sees’ an area of a US Class-A pan equal to [0.31 cos Q + 1.15 sin Q] m2, including what is seen of the wall. Integration of the expression over a whole day, for the case of the Sun at the equator at the time of the equinox (when the Sun rises to 90 degrees at noon), shows that the subtended area is 1.27 times the area of the water alone, on average. This ratio may be called the ‘pan radiation factor’ P. (The integration of the bracketed sum can be done by calculating Q for each hour of the day at any particular latitude A [13] and then adding the daily total. This is compared with the similar integral of [1.15 sin Q], to obtain P.) For these calculations it is assumed as an approximation that each daytime lasts twelve hours, the annual average.

The annual swing of the Sun's path between the Tropics means that P at latitude 38o, for instance, ranges from 1.35, the value at 15o (ie 38 - 23) in summer, to 1.66 at 61o (ie 38 + 23) in winter. However, once again we will take the average throughout the year, the value for 38o in this case, which is 1.46.

The annual average departure from overhead of the Sun's midday angle varies from 11.7 degrees at the equator (ie half the angle of the Tropics), to 13.9 at 10o latitude, 16.5 at 15o, and 20.3 at 20o. In other words, the average departure at 10o, say, is what it would be at 13.9o if there were no annual swing of the Sun's path. In general, it can be shown graphically that the average departure from the equator at latitudes between the Tropics is about [(23.5 + A)2 + (23.5 - A)2]/[4 x 23.5]. This correction at low latitudes has been incorporated into the following equation, fitted to calculations of P for various latitudes -

This is not an empirical equation, based on measurements of radiation, but is simply shorthand for the theoretically determined value of P.

The fraction f of direct radiation in the ground’s solar irradiance Rs depends on the cloudiness C. Hence the total direct component of solar irradiance, expressed in terms of the pan-water's area, is f.P.Rs, and the direct irradiance of the wall of the pan is f.(P - 1).Rs. As a first approximation, we may take f as proportional to the fraction of the sky that is not covered by cloud, eg 0.9 (1 - C/8). Then an expression relating C to the attenuation of extra-terrestrial radiation Ra in penetrating to the ground (Appendix 2) allows f to be expressed as equal to (2 Rs/Ra - 1.5).

b) Now consider the diffuse short-wave radiation on to the sides, which we will assume is isotropic. The amount depends on the fact that the wall is equally exposed to the sky above and the ground below, ie half of the wall's area is exposed wholly and exclusively to each source. As a result, the diffuse radiation from the sky consists of 0.5.(1 - f).Rs x 0.97/1.15, over the area of the water's surface. That equals 0.42 (1 - f).Rs.

The above three sections show that in total the ‘augmented shortwave solar irradiance’ Rs of the pan is as follows -

d) Where the surroundings of a pan are dry, they are warmer, for lack of evaporative cooling. (The criterion of dryness is discussed below.) This leads to additional longwave radiation to the wall, amounting to [(0.36.Rs - 36) / u] W.m-2 (see Appendix 3).

There remains one more consideration, the effect of elevation on the ground’s irradiation Rs. The intensity at sea level can be calculated in many ways [13], but most simply by two methods, A and B, described in a previous paper [12]. Then the result has to be multiplied by a height factor H, to allow for the thinner air layer above elevated sites. At sea level, the extra-terrestrial radiation Ra is reduced by a clear sky to about 0.75 Ra [13]. Therefore, at a height of 500 hPa (ie about 5,000 m) the reduction is to 0.87 Ra, if it is regarded as approximately linearly related to height z. In other words, the radiation intensity Rs has to be increased by a factor H equal to (1.0 + 3.2 x 10-5 z), which differs significantly from unity if z is above about 600 m.

In the present paper we use winds measured at 2 metres above the ground, since an US Class-A pan is often equipped with an anemometer at that height. Where winds are measured at other heights, they must be corrected. For instance, the wind at 2 m is about 0.73 times that at 10 m, or 1.6 times that at 0.5 m [13].

It was shown by Dale & Scheeringa [23] that dryness of the ground around a pan increases the evaporation rate. This may be attributed to the ground's longwave irradiance of the wall of a pan, considered already, and to the higher reflectivity of dry bare ground. There seems no other problem in applying Penman's equation in arid circumstances.

An area may be considered ‘dry’ if the ground desiccates to the extent that vegetation dies. Such dryness occurs when the monthly precipitation Pr is much less than local lake evaporation - below half, say. The lake evaporation rate is roughly equal to 5 T mm per month, where T is the monthly mean Celsius temperature [13, 24), so it is proposed that a month is 'dry' if Pr below 2.5 T. (This resembles Koeppen's criterion for a desert, ie Pr less than [2.4 T + 12] mm/mo [25]). Alternatively, the area is arid if the annual rainfall is less than 30 T, where T is the annual mean temperature.

The albedo of bare ground around a pan in arid country may be as high as 0.30, depending on the colour of the soil. If it is 0.30, the energy input to the pan is increased by 0.03 Rs W.m-2 (ie 0.97 x [0.30 - 0.22] Rs / 1.15) on account of the albedo being higher than that of grass. But this is usually trivial.

Since the resistance impeding water loss from a pan is greater than that impeding heat transfer from the pan, the appropriate version of Penman's equation is the same as that for a leaf [26 - 30] -

The net-irradiance term Rn in Eqn 4 is derived from a linear relationship with the solar irradiance Rs [13]. For a grass surface, Rn is given by [0.63 Rs - 40] W.m-2, and presumably [0.8 Rs - 40] for a water surface because of its lower albedo [12]. The albedo of a pan is halfway between the respective values for water and green vegetation [13], so the appropriate expression is taken as [0.71 Rs - 40] W.m-2, where the value of Rs to take here is H.Rs, the augmented value adjusted for elevation.

The outcome of the considerations above is the following version of Eqn 1, for the pan evaporation rate Ep at Melbourne, for instance (see Appendix 4) -

where T is the mean temperature, Td the dewpoint, u the wind speed, and s the slope of the psychrometric curve at temperature T. This might be called the Penpan equation’ for Melbourne, and is as simple as Eqn 1.

Evaporation estimates have also been made for eight other widely-spaced places, within the range of 22 - 44 degrees of latitude (Table 1). The procedure for developing the Penpan equation for Merna (an elevated, occasionally dry place in Wyoming) is outlined in Appendix 5.

Values from Eqn 5 are compared with measurements in Fig 2. The average error of monthly estimates is 0.49 mm.d-1, which is about 12% of the mean rate of 4.24 mm.d-1 measured by McIlroy & Angus [31] over three particular years.

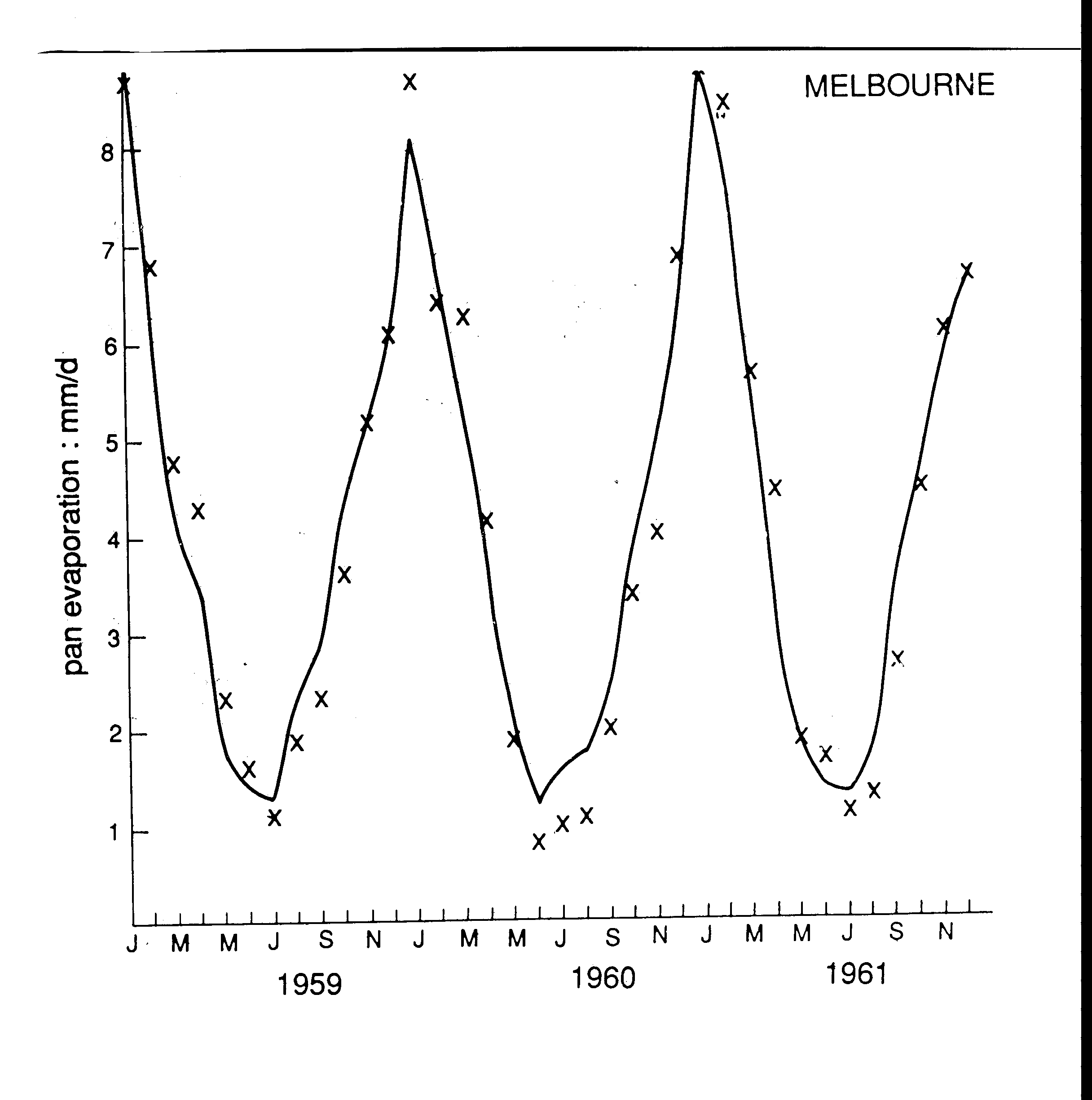
Fig 2. Comparison of estimates (crosses) from Eqn 5 with measurements (continuous line) obtained in 1959-1961 with a US Class-A pan evaporimeter at Melbourne [31]. .

The results from the eight other places are shown in Fig 3. The points lie much closer to a straight line than those in Fig 1. Also, deviations from the line representing equality of estimate and measurement are hardly proportional to the evaporation rate. This supports discussing estimate accuracy in terms of the average absolute, rather than the proportional error.

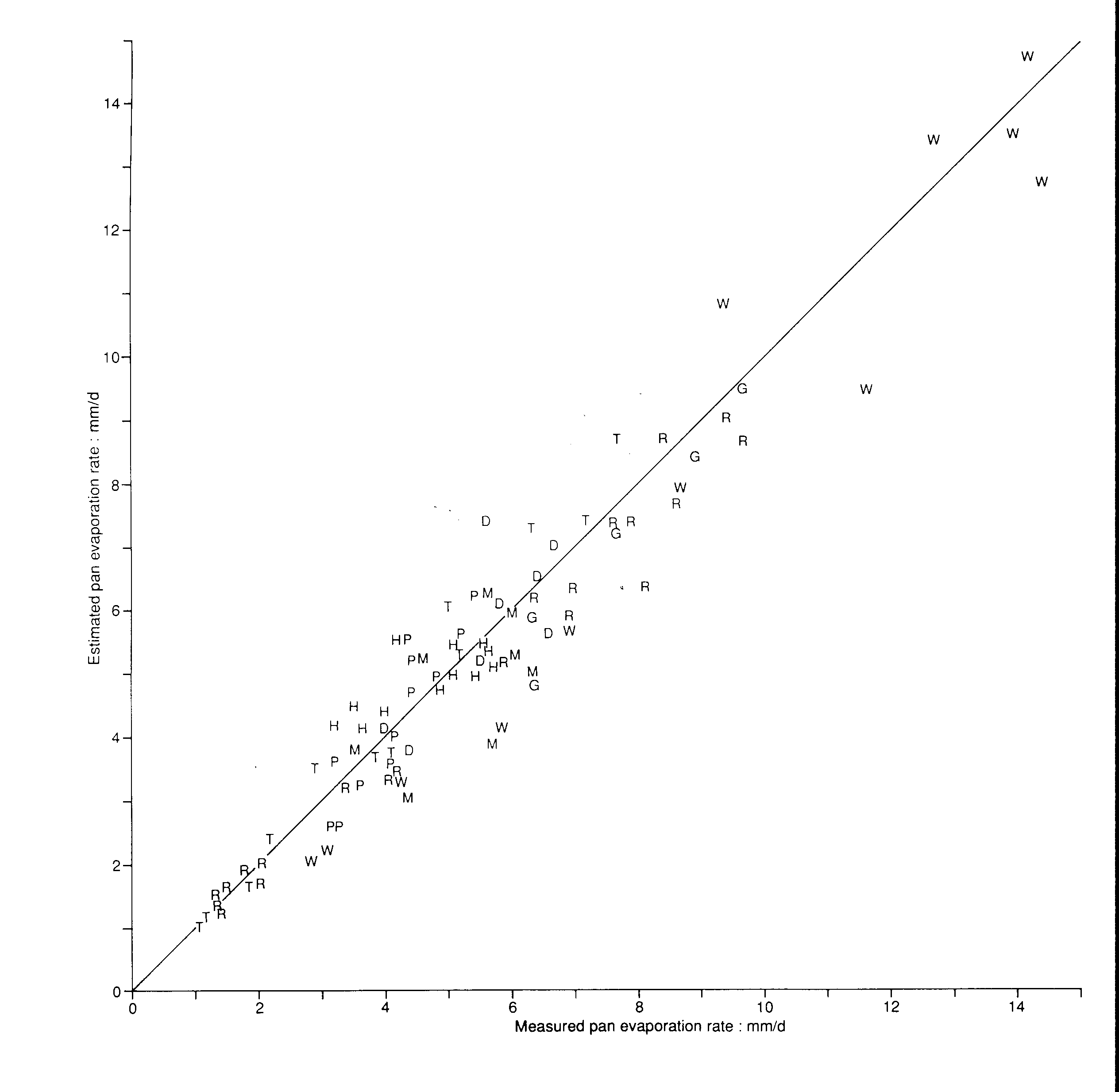
Fig 3. Comparison of estimated monthly mean evaporation rates with values measured at various places described in Table 1. The symbol D stands for Daniel (Wyoming), G for Gillette (Wyoming), H for Hong Kong, M for Merna (Wyoming), P for Pietermaritzburg (South Africa), R for Griffith (New South Wales), T for Mount Gambier (South Australia), W for Woomera (South Australia). The straight line shows where points lie if estimates equal measurements.

The median error in Table 1 is 0.55 mm.d-1, resembling the 0.49 mm.d-1 from Fig 2. In round terms, the error is about 0.6 mm.d-1, which is less than 10% of the midrange of Fig 3. Method B of estimating Rs yields lower evaporation-estimate errors in Table 1, except in the case of Woomera.

1. The ratio Eo/Ep is about 0.77, where Eo is the rate of evaporation from a lake and Ep from a US Class-A pan evaporimeter. However, this ratio varies with several factors, including the evaporation rate.

2. The value of Ep depends on the solar irradiance Rs of the pan, which in turn depends on the pan's geometry, latitude, elevation and solar declination, and the amount of cloud. These factors have been allowed for in developing equations based on Penman's formula, for estimating Ep.

3. Dryness of bare ground around a pan alters the albedo and temperature of the surface, and hence also affects the pan's irradiance, ie its evaporation rate. Such dryness is indicated by a monthly rainfall (mm) less than 2.5 times the mean temperature (oC).

4. A so-called ‘Penpan equation’ for estimating pan evaporation, based on method A of estimating solar radiation, requires only temperature data as essential input, though wind data are desirable in addition. However, it is less accurate than an equation based on method B, involving extra-terrestrial radiation and rainfall measurements. In general, the error of estimation is around 0.6 mm.d-1.

Acknowledgments The drawings were kindly made by Kevin Cowan of the Geography Department of the Australian National University. As regards Table 1, I am obliged to the South Australian Country Fire Service for the data from the Australian Bureau of Meteorology, to Dr L. O. Pochop for those from Merna and Daniel, and to Dr Bruce Clemence for those from Pietermaritzburg in South Africa.

Young [34] (77%, 77%), Penman [10] (78%), Kohler et al. [6] (60% - 82%), Harbeck [35] (69%), Nordensen & Baker [36] (74%), Nimmo [37] (61% - 79%), Sellers [38] (82%), Webb [39] (70%), Stanhill [40] (67%), Stanhill [16] (70%), Allen & Crow [7] (75% - 78%), Ficke [41] (76%), Hounam [8] (72%, 80%), Neuwirth [42] (72%), Hoy [43] (78%), Garrett & Hoy [44] (63% - 94%), Linsley et al. [45] (73%, 71%), Duru [46] (79%).

It has been shown elsewhere [13] that the extra-terrestrial radiation Ra is reduced to the ground-level value Rs according to the cloudiness, approximately as follows -

Rs = Ra ( 0.85 - 0.047 C) W/m2 (2.1)

Hence C = (0.85 - Rs / Ra) / 0.047 = 18 - 21 Rs / Ra

Thus the fraction f = 0.9 (1 - C/8) = 2 Rs / Ra - 1.5

There is a net transfer of longwave radiant heat between the ground and the side of a pan, because of any temperature difference. A difference arises from a lack of any evaporative cooling of the ground, when the climate is arid. In that case, all the net irradiance of the ground's surface Rg is converted into upwards convection of sensible heat (apart from daily cyclic flows between the surface and lower levels of the ground). Consequently, there is a warming of the surface by Rg/h', where h' (W.m-2.K-1) is the heat transfer coefficient between the air and the ground. The coefficient depends on the ground's roughness, but is typically about 4 u W.m-2.K-1 [13].

Pan-wall and air temperatures are similar, because of the evaporation from the water surface. The net longwave flux between surfaces which face each other is about 5 W.m-2 for each degree difference [13, 47], but this has to be halved in the case of a pan, because in effect only half the wall faces the ground, being at right-angles to it. So, for each degree difference, there is a flux (in terms of the pan's water-surface area) of about 2.1 W.m-2 (ie 0.5 x 5 x 0.97/1.15). Thus, the extra longwave irradiance from a bare dry environment Li is [(0.36 Rs - 36) / u] W.m-2. Such is the extra longwave irradiance to be considered when conditions are dry, to be added to the calculated net irradiance of the pan.

In view of the various considerations above, Eqn 4 becomes the following -

where F is the same as in Eqn 1. The number 68 is 28.4 x (200 + 280)/200, and 28.4 arises from the conversion of units from W.m-2 to mm.d-1. The net irradiance Rn is [0.71 Rs + Li - 40] W.m-2, as discussed in the text, where Li is the longwave increment (Appendix 3).

As an example, values (shown bold) are derived at each stage for the case of a pan at Melbourne. This is at latitude 38oS, near sea level and about 60 km downwind of the ocean. The annual mean temperature there T is 16.0oC.

ii) Calculate F from the following [12]:- [1.0 - 8.7 10-5 z]. 1.0

iii) Reckon f as 0.2, 0.5 or 0.8 according to whether the month's weather is wet and cloudy, average or dry, respectively. 0.5

iv) Obtain P from Eqn 2:- [1.32 + 4 x 10-4 A + 8 x 10-5 A2]. 1.44

vi) Hence derive Rs/Rs from Eqn 3 1.52

vii) Use the above ratio to determine Rs from an estimate of the monthly mean solar irradiance of the ground Rs obtained by one of the methods described elsewhere [12, 13], as follows -

Method A

If only daily extreme temperatures are available, take their average as the daily mean, whose average over a month is T. Hence find the annual mean T. 16.0

Then deduce the approximate annual mean irradiance Ry from the following [12, 48]:-

[210 + 1.8 A - 0.06 A2] W.m-2 191*

(*This agrees with the measured three-year average of 193 W.m-2 reported by McIlroy & Angus [31]).

Next derive the annual range of monthly mean temperatures DT, either from measurements (which is preferable) or from this approximate relationship with latitude and distance downwind of the ocean (d km) [12]:-

DT = 0.13 A.d0.2 degrees 11

Also calculate the annual range of irradiance DR, using the following empirical approximation [12] :-

DR = [60 + 4.A] W.m-2 212

Hence the month's deviation of irradiance q from the annual mean is as follows [12]:-

q = DR (T - T) / DT W.m-2 [19.3 T - 308]

The monthly mean solar irradiance Rs at sea level is Ry plus q

W.m-2 [19.3 T - 117]

This needs adjustment for elevation (z metres), i.e. multiplication by the height factor H , equal to (1.0 + 3.2 x 10-5z) 1.0

This is more accurate than Method A, because it incorporates additional information on monthly rainfall Pr mm, replacing temperature as the proxy for irradiance measurements. Method B also involves the cloudiness C (in tenths, approximately equal to [1 + 0.5 log Pr + {log Pr}2] ) and the extra-terrestrial radiation Ra, published in a table for any particular month and latitude [13]. The solar irradiance Rs is approximately as follows [13]:-

Rs = [Ra (0.85 - 0.047 C)] W.m-2 (4.2)

viii) Now correct for the reduced attenuation of the atmosphere above sites higher than 600m, by multiplying by the height factor H, given above.

ix) The radiation to a pan involves an augmentation of Rs by a factor given by Eqn 3, as mentioned in the text. So the corrected, augmented irradiance Rs is this for Melbourne:-

x) Hence derive Rn for Eqn 4, i.e. [0.71 Rs - 40] W.m-2 [21T - 166]

But add [0.36 Rs. - 36]/u to the above value of Rn to allow for longwave radiation onto the walls of the pan, if the area is arid. This is the case when either the monthly rainfall is less than 2.5 T mm (where T is the monthly mean temperature), or the annual rainfall is below 30 T mm (where T is the annual mean).

xi) The expression above can be put into Eqn 4.1 to yield Eqn 6 in the text:-

Ep = [21 T - 166 + 6 F u (T - Td)/ {28 + 46/s}] mm.d-1

This involves the use of Method A for determining the solar irradiance, at a high elevation, with aridity in some months.

Ep = [0.71 Rs - 40 + 4.8 u F (T - Td) ]/[28 + 34/s] mm.d-1 (5.1)

where Rs = Ry + DR(T - T)/DT W.m-2 (5.3)

The monthly temperatures indicate that T is 1.3 oC. Hence:-

Rs = 176 + 232 T/25.4 - 232 x 1.3/25.4 = 9.9 T + 177 W.m-2 (5.4)

Thus, the augmented irradiance Rs = 1.54 Rs = 15.2 T + 272 W.m-2 (5.5)

Hence, the net irradiance:- Rn = 0.71 {15.2 T + 272} - 40 = 10.8 T + 153 W.m-2 (5.6)

This must be increased by the additional longwave irradiance in the two months reckoned as dry, ie by [0.36 (9.9 T + 177) - 36]/u ,

i.e. by [3.6 T + 28]/u = Li W.m-2 (5.7)

Ep = [10.8 T + 153 + Li +4.8 u (T - Td)]/[28 + 34/s] mm.d-1 (5.8)

1. Brutsaert, W.1982. Evaporation into the Atmosphere. (Reidel, Amsterdam) 299pp.

2. Doorenbos, J. and Pruitt, W.O. 1977. Guidelines for Predicting Crop Water Requirements. Irrigation. and Drainage Paper 24. (Food & Agriculture Organisation, United Nations, Rome) 144pp.

3. Hanson, C.L. and Rauzi, F. 1977. "Class A pan evaporation as affected by shelter, and a daily prediction equation". Agricultural Meteorology. 18: 27-35.

4. Bloemen, G.W. 1978. "A high-accuracy recording pan-evaporimeter and some of its possibilities." Journal of Hydrology 39: 159-173.

5. Cahoon, J.E., Costello, T.A. and Ferguson, J.A. 1991. "Estimating pan evaporation using limited meteorological observations." Agricultural and Forest Meteorology 55: 181-190.

6. Kohler, M.A., Nordenson, T.J. and Fox, W.E. 1955. Evaporation from pans and lakes. Research Paper 38 (U.S. Department of Commerce, Weather Bureau, Washington) 21pp.

7. Allen, J.B. and Crow, F.R. 1971. "Predicting lake evaporation by performance of evaporation ponds, pans and tanks." Transactions of the American Society of Agricultural Engineers 14,:458 - 463.

8. Hounam, C.E. 1973. Comparison between pan and lake evaporation. Technical Note 126 (World Meteorological Organisation, Geneva) 52pp.

9. Eagleman, J.R. 1967. "Pan evaporation, potential and actual evapotranspiration." Journal of Applied Meteorology 6: 482-488.

10. Penman, H.L. 1948. "Natural evaporation from open water, bare soil and grass." Proceedings of the Royal Society, London A193: 120-145.

11. Stanhill, G. 1976. The CIMO International Evaporimeter Comparisons. Publication 449 (World Meteorological Organisation, Geneva) 38pp.

12. Linacre, E.T. 1993. "Data-sparse estimation of lake evaporation using a simplified Penman equation." Agricultural and Forest Meteorology (in press).

13. Linacre, E.T. 1992. Climate Data & Resources. (Routledge, London) 366pp.

14. Linacre, E.T. and Hobbs, J.E. 1977. The Australian Climatic Environment. (Jacaranda Wiley, Brisbane) 354pp.

15. Campbell, R.B. and Phene, C.J. 1976. "Estimating potential evapotranspiration from screened pan evaporation." Agricultural Meteorology 16: 343-352.

16. Stanhill, G. 1970. "The heat and water balance of a fish pond in the Upper Galilee of Israel." Israel Journal of Agricultural Research 20: 21-39.

17. Howell, T.A., Phene, C.J. and Meek, D.W. 1983. "Evaporation from screened Class A pans in a semi arid climate." Agricultural Meteorology 29: 111-124.

18. Riley, J.J. 1966. "The heat balance of a Class-A evaporation pan." Water Resources Research 2: 223-226.

19. Linacre, E.T. 1969b "Net radiation to various surfaces." Journal of Applied Ecology 6: 61-75.

20. Garzoli, K.V. and Blackwell, J. 1981. "An analysis of the nocturnal heat loss from a single-skin plastic greenhouse." Journal of Agricultural Engineering Research 26: 203-214.

21. Petkovsek, Z. and Rakovec, J. 1983. "The influence of meteorological parameters on a flat-plate solar energy collector." Archivs fur Meteorology Geophysiks und Bioklimatology B33: 19-30.

22. Linacre, E.T. 1964b. "Heat and moisture transfer about pan evaporimeters." Australian Meteorological Magazine 45: 1-12.

23. Dale, R.F. and Scheeringa, K.L. 1977. "The effect of soil moisture on pan evaporation." Agricultural Meteorology 18: 463-474.

24. Linacre, E.T. 1963. "Determining evapotranspiration rates." Journal of the Australian Institute of Agricultural Science 29: 165-77.

25. Conrad, V. 1946. Methods in Climatology. (Harvard University Press) 228pp.

26. Slatyer, R.O. and McIlroy, I.C. 1961. Practical Microclimatology. (Australian Commonwealth Scientific and Industrial Research Organisation) 324pp.

27. Monteith, J.L. 1963. "Gas exchange in plant communities." See [49]

28. Linacre, E.T. 1964a. "Calculations of the transpiration rate and temperature of a leaf." Archiv fur Meteorology Geophysiks und Bioklimatology. B13: 391-399.

29. Monteith, J.L. "Evaporation and environment." Symposium of the Society for Experimental Biology, 1965 19 (Cambridge University Press) 205-234.

30. Webb, E.K. 1975. "Evaporation from catchments." Prediction in Catchment Hydrology (Australian Academy of Science, Canberra) 203-236.

31. McIlroy, I.C. and Angus, D.E. 1964. "Grass, water and soil evaporation at Aspendale." Agricultural Meteorology 1: 201-224.

32. Finkelstein, J. 1973. "Survey of New Zealand tank evaporation." Journal of Hydrology (New Zealand) 12: 119-131.

33. Thom, A.S., Thony, J.L. and Vauclin, M. 1981. "On the proper employment of evaporation pans and atmometers in estimating potential transpiration." Quarterly Journal of the Royal Meteorological Society, London 107: 711-736.

34. Young, A.A. 1947. "Some recent evaporation investigations." Transactions od the American Geophysical Union 28: 279-284.

35. Harbeck, G.E. 1958. Lake Hefner water-loss investigations. Publication 45 (International Association of Scientific Hydrology) 437-43.

36. Nordenson, T.J. and Baker, D.R. 1962. "Comparative evaluation of evaporation instruments." Journal of Geophysics Research 67: 671-679.

37. Nimmo, W.R. 1964. "Measurement of evaporation by pans and tanks." Australian Meteorological Magazine 46: 17-53.

38. Sellers, W.D. 1965. Physical Climatology. (Chicago University Press) 272pp.

39. Webb, E.K. 1966. "A pan-lake evaporation relationship." Journal of Hydrology, Amsterdam 4: 1-11.

40. Stanhill, G. 1969. "Evaporation from Lake Tiberias: an estimate by the combined water balance-mass transfer approach." Israel Journal of Earth Science 18: 101-108.

41. Ficke, J.F. 1972. Comparison of evaporation computation methods, Pretty Lake. Professional Paper 686-A (U.S. Geological Survey) 48pp.

42. Neuwirth, F. "Experiences with evaporation pans at a shallow steppe-lake in Austria." Hydrology of Lakes, Helsinki, 1973 (International Association of Hydrological Science) 290-297.

43. Hoy, R.D. "Pan and lake evaporation in Northern Australia." Proceedings of a Hydrology Symposium, Brisbane,. 1977 (Institute of Engineers, Australia) 57-61.

44. Garrett, D.R. and Hoy, R.D. 1978. A study of monthly lake to pan coefficients using a numerical lake model. Publication 78/9 (Institute of Engineers, Australia) 145-149.

45. Linsley, R.K., Kohler, M.A. and Paulhus, J.L.H. 1982. Hydrology for Engineers. (3rd edn, McGraw-Hill) 508 pp.

46. Duru, J.O. 1984. "Blaney-Morin Nigeria evapotranspiration model." Journal of Hydrology 70: 71-83.

47. Monteith, J.L. 1973. Principles of Environmental Physics. (Arnold) 241pp.

48. Linacre, E.T. 1969a. "Empirical relationships involving the global radiation intensity and ambient temperature at various latitudes and altitudes." Archiv fur Meteorology Geophysiks und Bioklimatology B12: 1-20.

49. Evans, L.T. (editor) 1963. Environmental Control of Plant Growth. (Academic Press) 448pp.

50. van Aken, J. and Fleming, P.M. 1968. Meteorological data 1931 - 1967 (Division of Irrigation Research, Commonwealth Scientific and Industrial Research Organisation) 35pp.

51. Chen, T.V. 1976. Evaporation and evapotranspiration in Hong Kong. Technical Note 42. (Royal Observatory, Hong Kong) 67pp.

Table 1. Details of the places mentioned in Fig 3. The elevation is given in metres, the rainfall in millimetres per annum and the mean estimation error for each place in mm.d-1.

(1) assumed

(2) the pan was surrounded by a light-coloured gravel

A - the latitude (degrees)

C - the cloudiness C expressed in ‘oktas’, ie in units of eighths of the sky’s area

C - the fraction of the sky occupied by cloud (oktas)

c - the specific heat of air, ie the amount of heat required to warm unit mass by one degree Celsius

d - day, eg ‘mm.d-1’ means millimetres per day

d - the distance (in kilometres) upwind to an ocean shore

DR - the difference between the monthly mean values of solar radiation Rs in the months with least and most, respectively

DT - the difference between the monthly mean temperatures of the hottest and coldest months, respectively

Eo - the evaporation rate of a lake (mm.d-1)

Ep - the evaporation rate of a US Class-A pan evaporimeter (mm.d-1)

EPen - the lake evaporation rate estimated from Penman’s formula (mm.d-1)

Et - the evaporation rate of a well-watered crop, ie the potential crop evaporation rate (mm.d-1)

F - a factor equal to [1.0 - 8.7 x 10-5 z], expressing the effect of elevation on atmospheric density, and hence on the convection of heat from a surface

f - the proportion of the solar radiation Rs which is direct from the Sun

H - the factor [1.0 + 3.2 x 10-5 z), expressing the effect of elevation on the solar radiation Rs

h - the convective heat-transfer coefficient, being a measure of the rate at which heat energy is transferred through unit area by convection

h’ - the coefficient of heat transfer between the ground and the atmosphere

hPa - hectopascal, the unit of atmospheric pressure (replacing the millibar)

K - degree Celsius difference

K-1 - per degree Celsius

L - the latent heat of water evaporation, ie the amount required to evaporate unit mass (Joules per kilogram)

Li - the extra longwave irradiance from a bare dry environment

m - metres

mm - millimetre

mo-1 - per month

P - the ‘pan radiation factor’, expressing the effect of the pan’s geometry on the solar radiation it intercepts, as a daily average

Pr - the monthly precipitation (mm)

Q - the angle of the Sun above the horizon, ie the Sun’s ‘elevation’

q - the difference between a month’s mean sea-level solar irradiance and the annual mean

Ra - the ‘extra-terrestrial’ radiation intensity, ie the intensity of solar radiation above the atmosphere, onto a surface parallel to the ground

ra - the resistance to either heat loss from a flat surface to the atmosphere

Rg - the value of Rn for ground’s surface

Rn - the net irradiance of a surface, being the difference between the incoming (shortwave and longwave) radiation and outgoing (reflected and emitted) radiation

Rs - daily mean solar irradiance of the ground

Rsl - the value of Rs at sea level

Rs - the ‘augmented shortwave solar radiation’, ie the sum of the three component fluxes to a US Class-A pan, viz the direct, the diffuse and the reflected fluxes

rs - the extra resistance (in addition to ra) impeding evaporation from a US Class-A pan, since evaporation takes place only from the water surface, whereas heat is lost more easily, from the walls of the pan also

Ry - the annual mean solar irradiance

s - the slope of a tangent to the ‘psychrometric curve’, a graph of saturated water-vapour pressure against temperature

s.m-1 - seconds per metre, a unit of the rersistance to heat transfer

T - daily mean Celsius temperature

T - the annual mean temperature

Td - the daily mean dewpoint temperature

u - daily mean wind speed (metres per second)

W.m-2 - watts per square metre, a unit of energy flux

z - elevation (metres)

Copied by permission of the International Water Resources Association, 1101 West Peabody Drive, Urbana, Illinois, USA, 61801-4723. The paper is based Linacre (1994):

Linacre, E.T. 1994. Estimating U.S. Class-A pan evaporation from few climate data. Water International 19, 5 - 14.