|
E. Linacre |
4/'99 |
![]()
Summary
Fair success may be achieved in deducing the location of a place from a given small set of climatic data, using crude empirical relationships between climate and geographic averages. Conversely, monthly mean temperatures can be inferred approximately from geographic information. The extent to which these normative estimates differ from actuality offers clues on the effects on climate of regional features of topography and ocean circulation, as well as on microclimatic effects.
1. Geography and climate
It has long been assumed that climate is largely controlled by location or geography. In the sixth century BC, the Greek philosopher Pythagoras recognised the sphericity of the Earth and the dominance of latitude in explaining climate variation (Sanderson 1999). Two centuries later Aristotle expanded on Pythagoras's foundation and introduced five climate zones, ranging from tropical to northern frigid. It is not coincidental that in the early 20th century German scientist Koeppen also used 5 climate zones in his classification, identified with the letters A-E.
Koeppen's classification was developed at a time when it was widely believed, especially in the German scientific arena, that climate, and therefore geography determined flora and fauna, even the physical and behavioural traits of human societies. Obviously such determinism has its limitations, but it highlights the widespread and longstanding belief that location determines climate. More recent work by Geiger (1960) indicates that even the microclimate is largely controlled by the local 'geographical' conditions, such as orography and coastlines.
Given this control one could hypothesise that one can infer the place where given climatic data were obtained. In other words, can we work out the one or more locations where a station may be, even approximately, if we are given its climatic record? This is the key question addressed herein.
The basic information is outlined elsewhere (1). In brief, the main governing factors can be summarised as these -
These factors suggest that the following information should be sufficient (2):
Let us now consider possible guidelines about climate as a function of geography.
The annual mean temperature is given approximately by the average temperature of the maxima and minima for the warmest and coldest months, i.e. an average of four numbers. This temperature varies primarily with latitude (Fig 1), although warm and cold ocean currents can be identified in Fig 1. The western ocean margins (near the east coast of a continent) are warmer around 20-30° N or S, but they are colder around 40-50° N, when compared to the eastern margins (west coasts). Also, subtropical deserts are distinctly hot, on average.
Fig 1. Global distribution of annual mean temperature near sea level (click on image for more detail)(Source: NOAA-CIRES Climate Diagnostics Center, Boulder, Colorado).
Data from a large number of stations suggest that the annual mean temperature is around 27° C within 20° S - 16° N degrees and then falls by about 0.85 K/degree latitude in the northern hemisphere and 0.63 K/° lat in the south (Fig 2). This implies that on average the southern hemisphere is warmer than the northern hemisphere (17°C vs 11°C, respectively), which is true, if the Antarctic plateau stations are excluded, as in Fig 2. These stations are 30-40K colder than the curve in Fig 2 suggests, on account of their altitude and their isolation within the circumpolar vortex (3).
Thus a mean temperature of 19°C in the northern hemisphere is likely to be found at sea level at about 25° N (i.e. 16 + [27 - 19]/0.85). However, a lower latitude is possible if the place is elevated or near a cold ocean current; a place 1,000 metres high may be 4 K cooler on average than another at sea level and the same latitude (4). So a temperature of 19° C may be found below 16° N at 2,000 m elevation (i.e. 27 - 2,000[4/1,000]). Choosing between these alternatives is facilitated by considering the ‘annual range’ and monthly rainfalls.
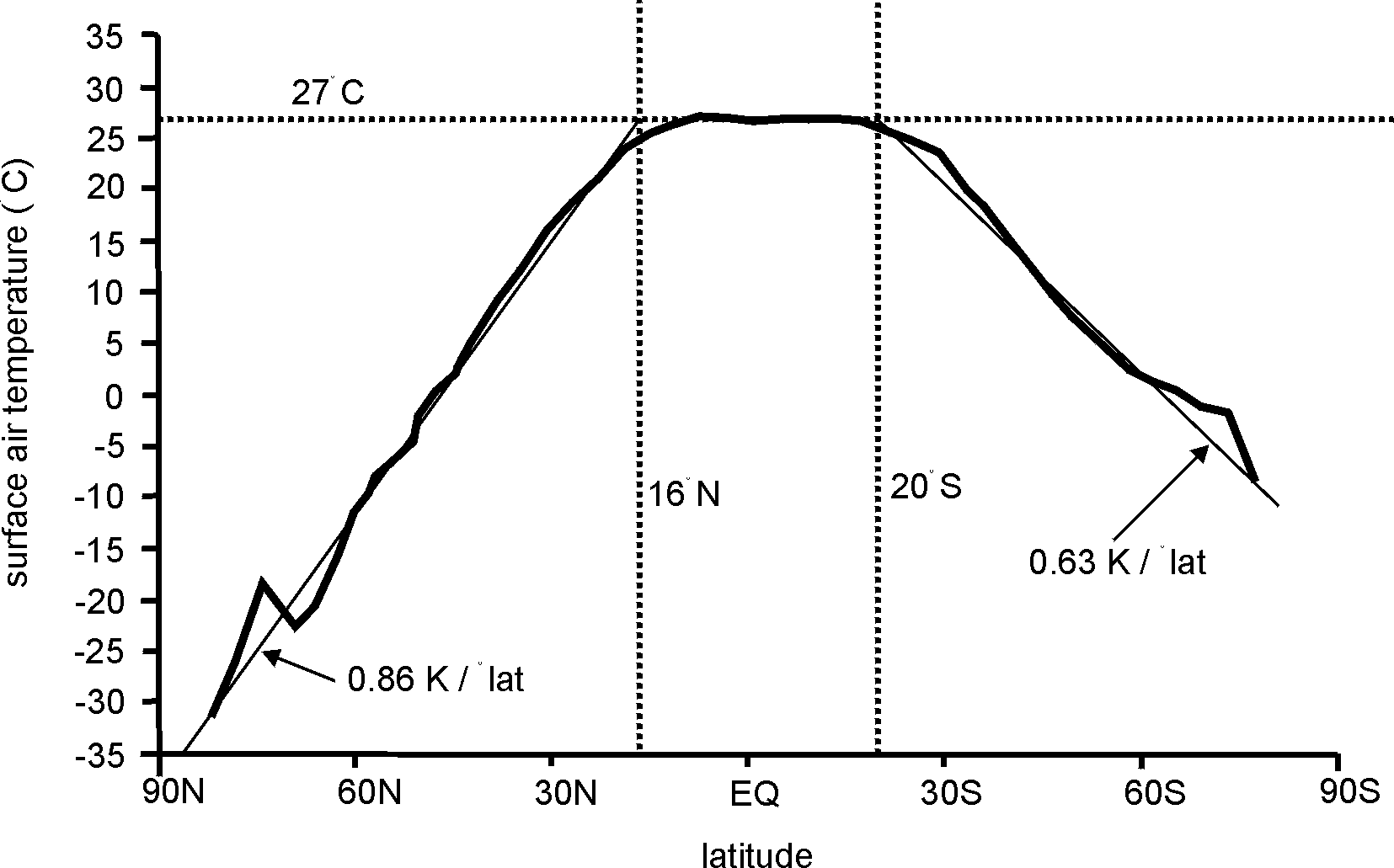
Fig 2. Mean temperatures at various latitudes (5). The straight lines have been superimposed.
The ‘annual range’ is defined as the difference between the hottest and coldest months, taking monthly mean temperatures in each case. It is given approximately by the difference between the average of the January maximum and minimum temperatures, and the corresponding average for July (6). We will call the January/July difference the ‘apparent annual range’. The error in assuming that the January and July temperatures are the hottest and coldest (or vice versa) is small at latitudes above about 40 degrees, but data from Africa, South America and Europe show that the true range exceeds the apparent range on average by about 1 K at latitudes 0 - 10, 1.5 K over 11 - 20 and 0.5 K over 21- 40 degrees.
The 11-20 degree belt generally experiences a wet season in the summer, so cloudiness and rain reduce the maximum temperature. The hottest month there usually falls 1-2 months before the summer solstice (i.e. April or May in the northern hemisphere), when the noon sun is near the zenith and the skies are often clear. Many places near a west coast in the 21- 40 degree belt are affected by low sea surface temperatures due to upwelling of deep-ocean water (7), and this upwelling is often most intense in summer, because the high pressure cell over the adjacent subtropical ocean is stronger. Therefore the warmest month here may be a few months after the summer solstice, e.g. September in the northern hemisphere.
A small annual range indicates either a low latitude and/or proximity to the sea (8, 9), especially on the coast facing the prevailing wind. Fig 3 shows this in South America, for example.
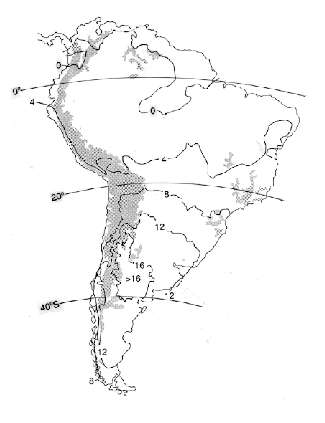
Fig 3. Variation of the annual range of temperature over South America.
The annual range is of the order of 0.4 times the latitude, e.g. about 16 K at 40 degrees latitude (see Fig 4). However, the scatter of crosses in Fig 4 indicates that this is a first-order estimate only. Most importantly, it ignores the effect of the distance from the sea.
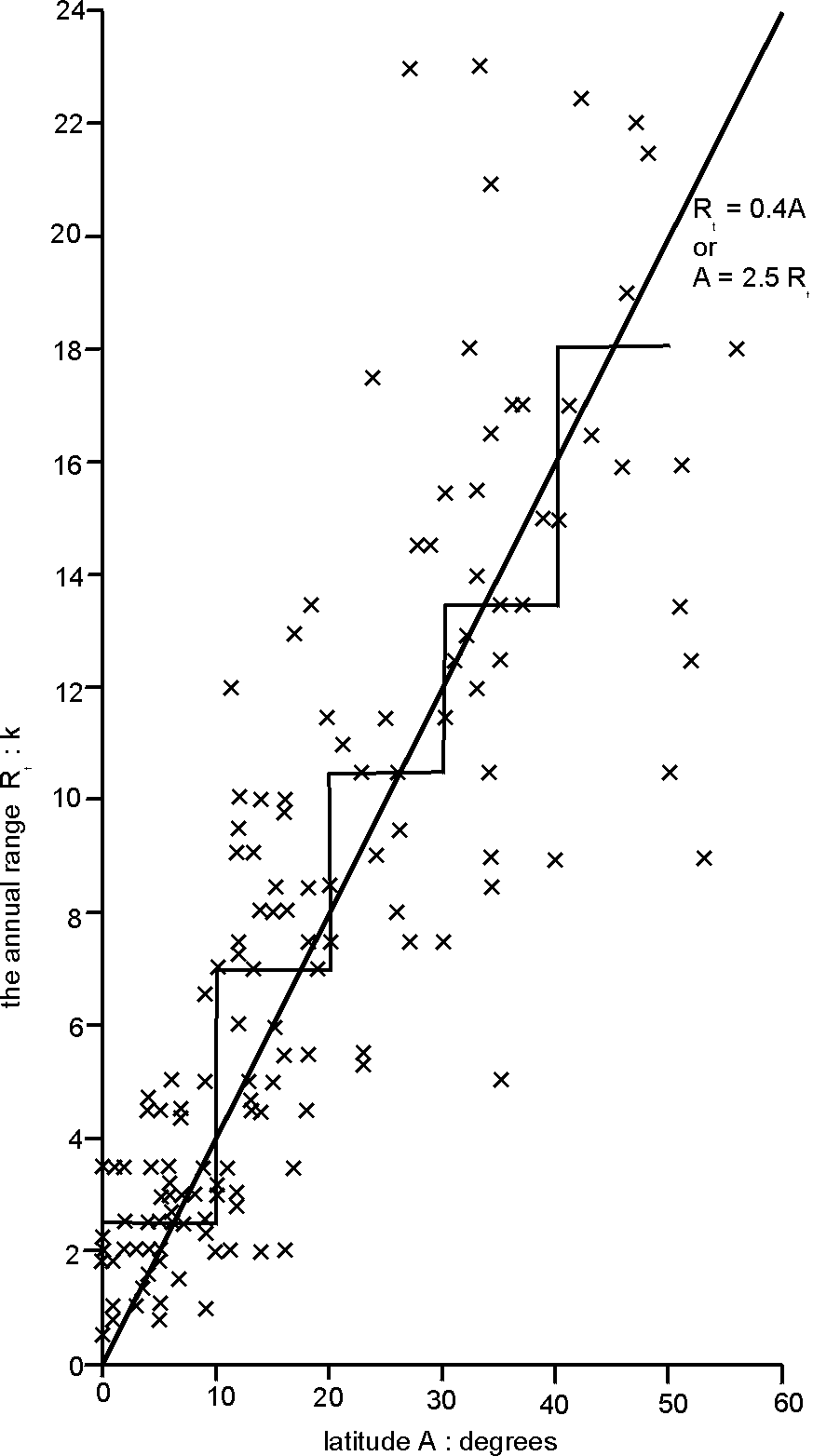
Fig 4. The variation of the annual range of temperature with latitude, using data from 142 places in Africa, South America and Europe (10).
As regards the effect of distance from the sea, consider, for example, places in Queensland at 27°S, at which latitude the wind is from the east. There we find an increase of annual range westwards. The range increases from 8 K by the ocean, to 12 K at 100 km inland, and 17 K beyond 400 km (11). On the other hand, the wind is mostly westerly at 42°N, so that Chicago lies about 3,000 km from the ocean (i.e. the Pacific) and therefore has a range of 28 K (6).
Overall, the apparent range Tr is given by this -
Tr = 0.13 A d0.2 K
where A is the latitude (degrees) and d is the distance downwind of the ocean (km). The equation is based on Fig 5, which shows a much better fit.
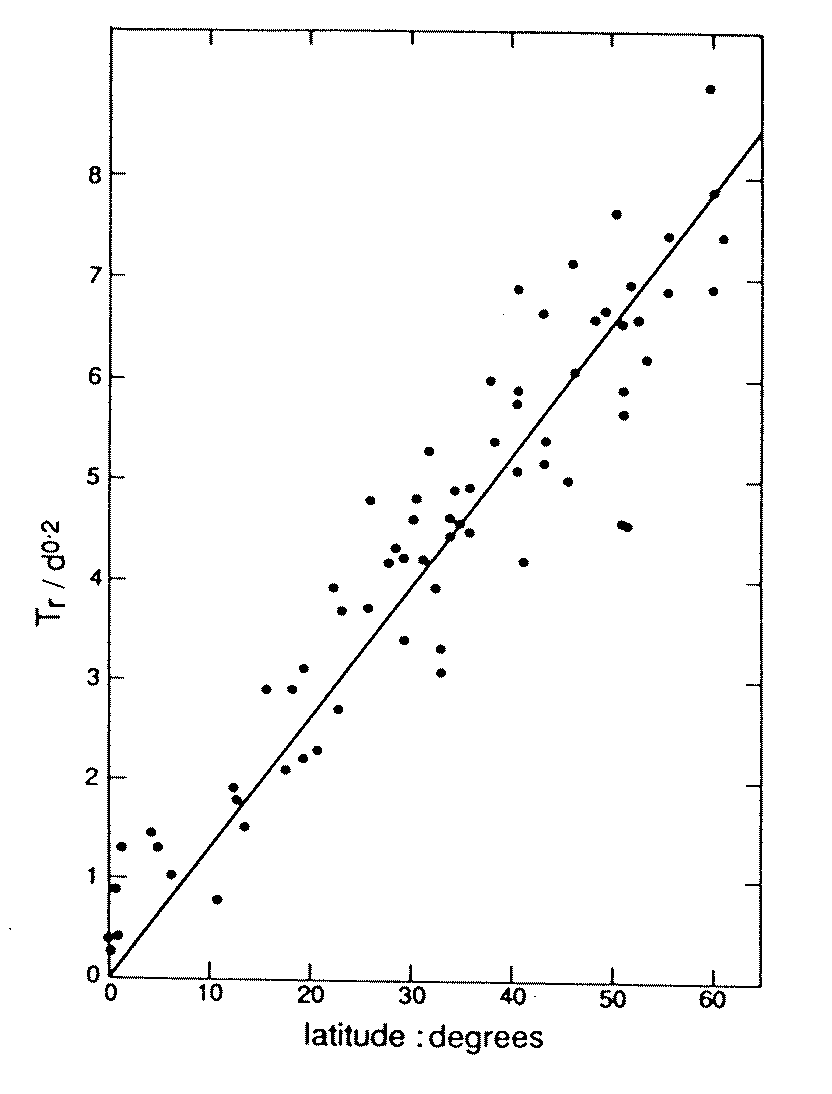
Fig 5. Relationship between the January/July temperature difference, the latitude A degrees and the distance downwind of the ocean d km (12).
The equation above means that the distance d can be estimated as follows
d = [Tr / 0.13 A]5 km
Most rain on earth is triggered by any of three uplift mechanisms, or a combination of them:
A wet summer and dry winter suggests a low-latitude zenithal-rain or monsoonal climate. The former, zenithal rain, is due to latitudinal shifts of the Inter-Tropical Convergence Zone (ITCZ) (13). The 'monsoonal' regime differs only from the more general zenithal-rain climate by the requirement that the surface winds change direction at least 120° between seasons (14). Monsoons generally occur between 10-30 degrees of the equator, but over a few degrees further north in late summer over India, and, especially, southern China.
Frontal precipitation falls at latitudes between about 35-70 degrees, but lower in winter. Between 30-40 degrees, mainly at west coasts, the rainfall in winter is much greater than in summer. This is because fronts stay poleward in summer. The rainfall is more uniformly distributed along east coasts and in the interior in this latitude belt, not because fronts do penetrate into these regions in summer, but because of convective rainfall.
The global average rainfall is 860 mm/a (15), i.e. about 70 mm/month, over oceans and land together. Precipitation is heaviest near the ITCZ and in areas where monsoon winds come from over a warm ocean. Arid conditions are generally found in the subtropics (mainly between 18-33° ) (except where the Trade winds blow onshore or where the monsoon penetrates further poleward) and near the poles (16).
Precipitation increases with elevation on the windward side of mountains up to about 2,000 metres, very approximately, and then decreases with height because of the cold air there, which cannot ‘hold’ much moisture (17). Rainfall is less on the lee side of a mountain, as in the case of the Patagonian desert in Argentina, to the east of the southern Andes, where the wind is from the west. It is also less in the Gobi desert in Mongolia, not only because monsoonal moisture is trapped by the Tibetan plateau, but also because frontal systems have lost most of their moisture on their long travel from the Atlantic.
Thus, dry conditions imply either a subtropical or polar latitude, an extreme elevation, a rain shadow, situation near an anomalously-cold ocean (e.g. the Atacama desert in northern Chile) and/or great distance downwind of the ocean. Such conditions are indicated by low rainfall figures and a large daily range of temperatures (18).
d) Daily temperature range
The daily range of temperature is the difference between the maximum and minimum temperatures in 24 hours. It has no meaning at latitudes above 66.5 degrees, where the Sun does not appear for 24 hours during the winter solstice. If the daily range is large, the atmosphere is dry (18) and there is little cloud, probably indicated by low rainfall figures. Thus a large range may indicate a position well inland, considerable elevation above cloud level, and/or a latitude near the Tropics, where anticyclones are common. Within anticyclones the air is dry and the sky often cloud-free; also, there is little wind, allowing the build-up of a strong nocturnal radiation inversion. Near the ITCZ and in areas frequented by frontal systems, not only does cloudiness limit daytime heating and nighttime cooling, but also, the air is too humid to cool much at night (near the ITCZ) or too windy (at mid-latitudes).
There appears to be no systematic variation of the annual mean daily range with latitude (e.g. reference 19), because of the annual movement of the ITCZ, and the key dependence of a station's location on a continent.
The effect of the station elevation (h, in km) can be isolated: there is a slight tendency for the daily range to be given by this (Fig 6)-
Rd = 8 + 2 h K
This equation means that a range of 12 K, say, suggests (very tentatively) an elevation of 2 km, i.e. [12 - 8] / 2 . However, it would be better to use Fig 6 directly, as a guide to Rd; in that case, the deduced elevation for a daily range of 12 K would be about 1 km. The broad scatter in Fig 6 is not surprising: a place on the windward side of mountains has a much smaller daily range than a place at the same elevation on the lee side.
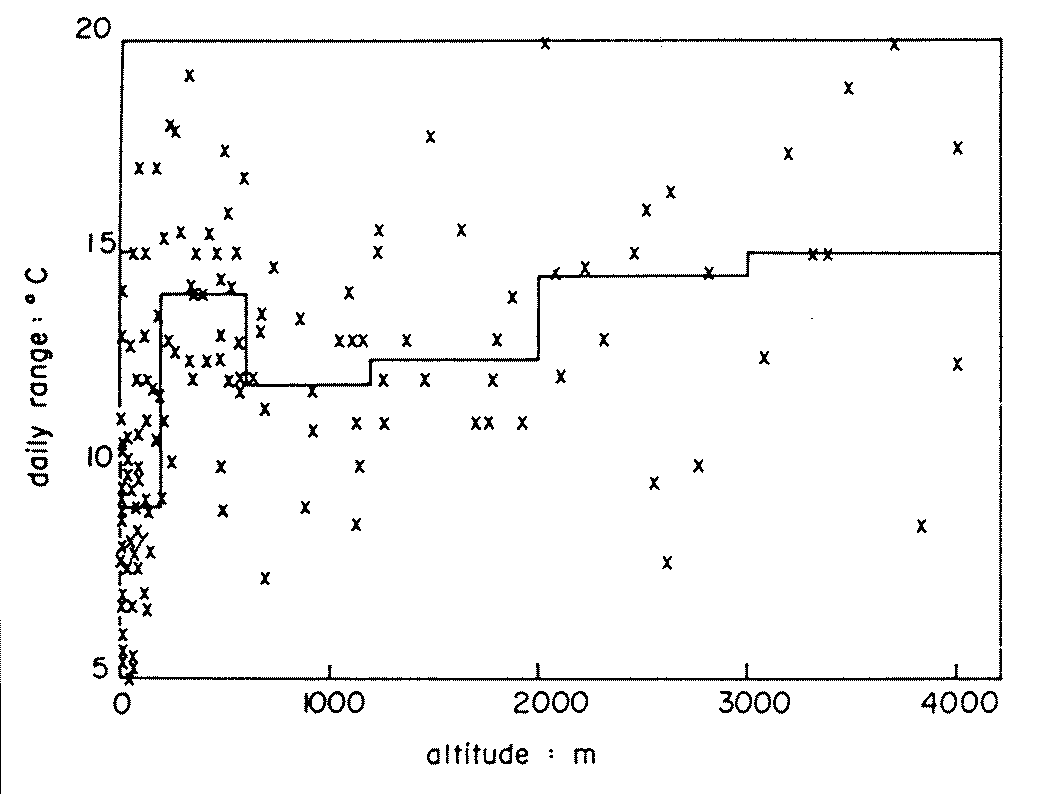
Fig 6. Daily ranges at various elevations (20). The horizontal lines show the median values for each band of elevations.
A rough connection between rainfall P (mm/month) and daily range is shown in Fig 7, yielding the very approximate equation -
Rd = 13.5 - 2 log P K
Estimates of Rd from this may be compared with that from the relationship with elevation. Unfortunately, this formula is of little use for estimating P, for instance, not only because of the great scatter seen in Fig 7, but also because of the formula’s nature; a small error in Rd leads to a huge difference to the value of P.
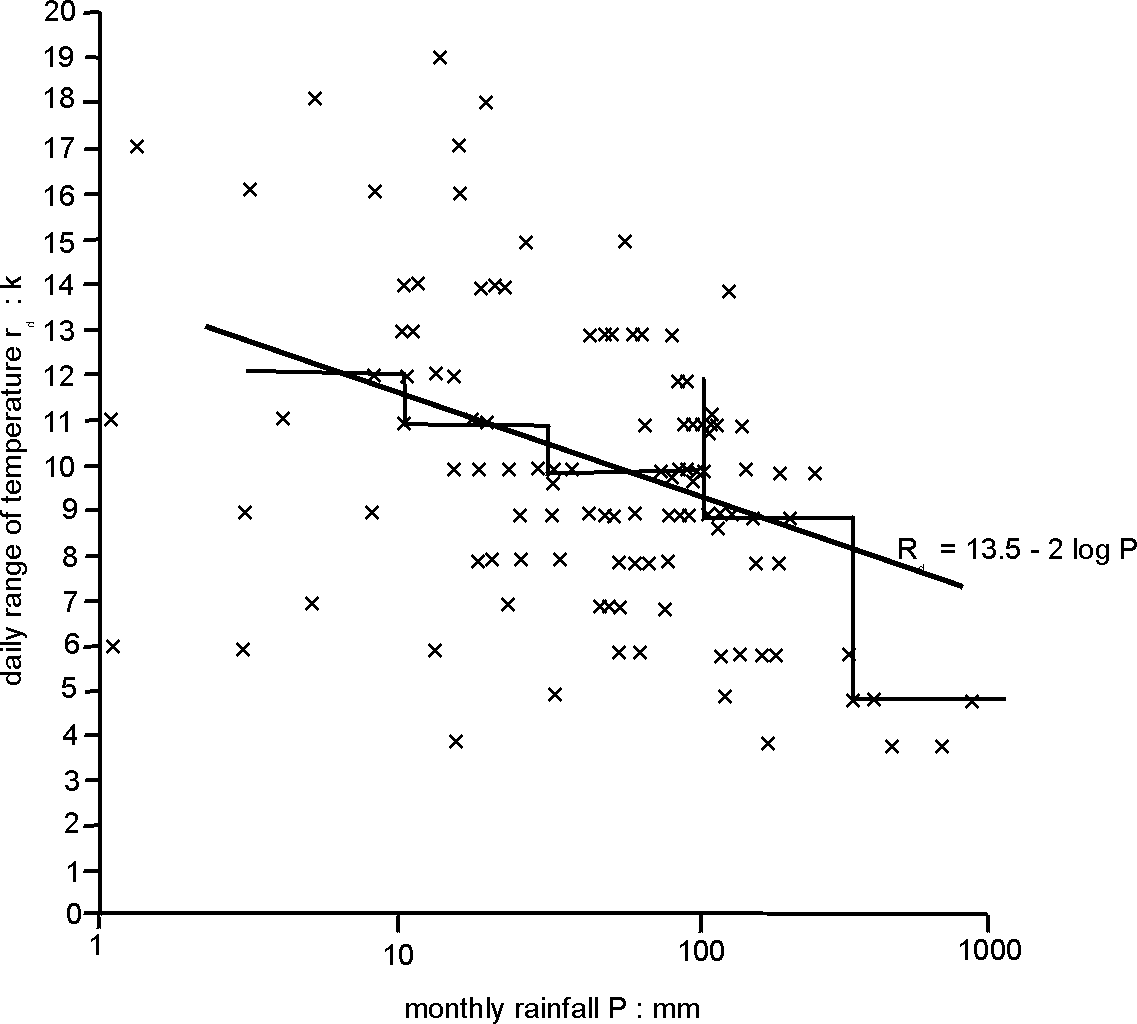
Fig 7. Connection between the monthly mean daily range of temperatures Rd (K) and the monthly rainfall P (mm), using 114 values from the USA, India and China (10). The horizontal lines show the median value for each band of rainfalls.
e) Surface wind
The prevailing wind direction has been mentioned several times as indirectly important in determining the climate. It affects whether the incoming wind is cooled by an west-coast ocean current, it governs whether or not a place is dry because it is far from the upwind ocean (as in the Gobi desert, for instance), it determines whether a place is dry because it lies in the lee of a high mountain range or wet because the wind has lately come from a warm ocean.
The direction of the wind depends primarily on the latitude, which is assumed already assessed, at least provisionally, from consideration of the annual temperature mean and range, and precipitation. Winds tend to be light and variable from the equator to about 10 degrees latitude, generally easterly and steady over 10 - 25 degrees, variable between 25 - 35 degrees, mainly westerly but variable over 35 - 60 degrees, variable between 60 and 70 degrees, and easterly nearer the pole (21, 22). Also note what has been said about monsoonal climates.
2. Procedure
In view of all this, one proceeds to estimate the location of the place with a given climate by calculating the annual mean temperature, the annual range and daily range, and by examining the rainfall figures. Then write down the respective implications of each of these figures, in the light of the considerations above. First try to assess the possible latitude, then the possible elevation, then the distance inland. Finally, from the assessed figure for the latitude, deduce the implied wind direction and check that this is consistent with the temperatures and rainfall at the place provisionally selected.
But bear in mind that local topography may confuse the issue, so that no estimate can be more than indicative.
Example 1
Let us take the case of a place with an annual average temperature T of 12° C, a January/July difference of 3.5 K and rainfall of 163 mm in January and 5 mm in July. The daily range is 13 K in January and 22 K in July, i.e. around 17 K.
Thus we estimate a place around 11° S, 3.7 km high and roughly 100 km from the coast. It is actually Cuzco in Peru, at 13° S, 3.2 km high, and about 350 km inland.
Example 2
The opposite kind of estimate is also possible, the determination of approximate temperatures for a given locale. For instance, take Chicago, which is at 42° N, 250 m elevation and about 3000 km downwind of the Pacific ocean (but only 1400 km from the Gulf of Mexico). The sea-level temperature is estimated to be 5° C, i.e. (27 - 0.85 x [42 - 16]) . However, the height means that the value has to be reduced to 4° C, i.e. 8 - 250 x 4/1000. The formula for the annual range shows it to be 23-27 K, i.e. 0.13 x 42 x d0.2, where d is either 1400 (less common) or 3000 km (more common). Thus the January and July monthly mean temperatures would be about (4 - 26/2) and (4 + 26/2), respectively, i.e. -9° C and 17° C. The observed figures are -4° C and 23° C, both about 5 K higher than the estimates. This is warmer than expected, mainly because of the moderating influence of Lake Michigan (in winter) and warm advection from the Gulf of Mexico (in summer).
It is harder to derive the daily range because of the large scatter in Fig 6. For what it is worth, the estimate from Fig 6 is 13 K, which is more than the observed values of 8 K in both January and July. We hypothesise that the daily ranges are reduced by strong winds in winter and the high humidity in summer.
3. Conclusions
These examples illustrate how far empirical relationships between elements of climate and geography can be used to estimate either location or climate from the other. It is interesting to see how much can be deduced, even when ignoring local circumstances. Their importance can be assessed by comparing the normative estimates against actual observations.
Ideally, the procedures for estimating either geography or climate norms from the other would be simplified into the format of a decision tree, ready for the development of a computer program - or even a board game?
Acknowledgements: Fig 3 was provided by Dr Peter Jones of Centro Internacional de Agricultura Tropical, Cali, Colombia.
References