|
B. Geerts and E. Linacre |
12/'97 |
The net mass convergence into a column of air (from the surface to the tropopause) is generally much smaller than the convergence at any particular level. This is beacuse convergence at one level tends to be offset by divergence at another. This is known as Dines compensation (Note 12.G). Mathematically this principle is explained by the continuity of air:
|
r (¶ u/¶ x + ¶ v/¶ y) = ¶ (rw)/¶ z |
kg m-3 s-1 |
(this is the Boussinesq form of the mass continuity equation) where (u,v,w) are the 3D velocity components in directions (x,y,z) and r(z) is the air density. The term (¶ u/¶ x + ¶ v/¶ y) is the horizontal divergence; convergence occurs when this term is negative. An integration of this equation with height, subject to zero vertical motion as boundary condition at the top and bottom, yields:
|
ò r (¶ u/¶ x + ¶ v/¶ y) dz = 0 |
i.e. mass divergence at some levels must be offset by convergence at others |
Physically, compensation occurs because convergence in the lower troposphere implies that air in the atmospheric column must ascend. However, very little air escapes through the tropopause into the stratosphere, and the height of the tropopause does not change much. Therefore the uplifted air must spread out somewhere below the tropopause. Therefore, low-level convergence implies divergence somewhere aloft in the troposphere, i.e. Dines compensation
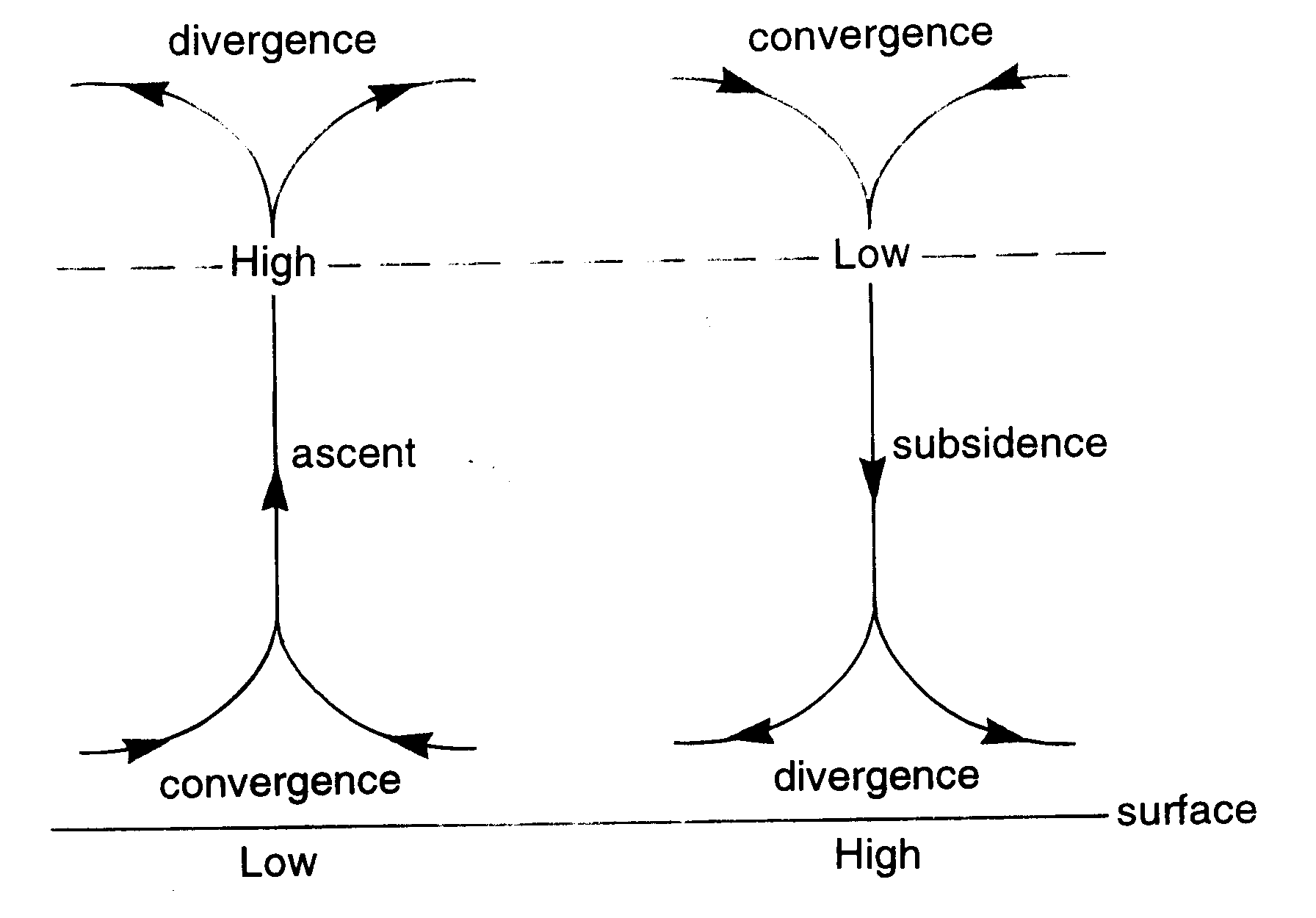
Various configurations are possible, but the two most relevant ones are shown in Fig 1. Low-level convergence (divergence) and atmospheric ascent (subsidence) occur along with the counterpart at a higher level. This principle applies to the convective scale: thunderstorm updrafts gather air in the boundary layer and rapidly lift it into the upper troposphere. A thunderstorm anvil dramatically displays the divergence aloft. On the synoptic scale, surface friction causes low-level convergence into a low-pressure region (or trough), as explained in Fig 12.9c. Similarly, divergence occurs from a surface high or ridge, as air trajectories cross the isobars towards a lower pressure.
Dines compensation implies a relationship between convergence (assessed from surface winds) and vertical motion. Synoptic vertical motion is far too slow to measure directly (it is around 0.01 m/s, up to 0.1 m/s in vigorous frontal disturbances), yet it is essential to weather, since ascent leads to clouds and precipitation, whereas descent leads to clear skies.
At mid-latitudes the weather systems are largely driven by wind patterns in the upper troposphere, in particular the Rossby waves and jet streaks. These produce upper-level divergence (hence uplift and inclement weather) in some areas and upper-level convergence (hence subsidence and fine weather) in other regions. This is discussed further in Note 12.L.

Fig 1 Dines compensation applied to large-scale circulations in the tropics. However, large-scale mid-latitude circulations are different: they do not have an upper-tropospheric high (ridge) above ascent regions , or a low (trough) above areas of subsidence.