E. Linacre and B. Geerts

4/'00

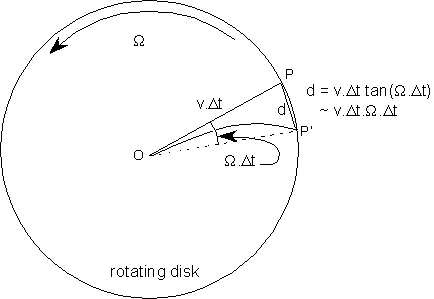
Consider an object travelling from the centre (point O) towards P on the edge of a rotating disk (Fig 1). It takes time Dt when travelling at speed v, so the distance OP equals v. Dt . However, after a time Dt, P will have moved from its original position (P') to a new position (P). The angle POP' equals t times the speed of rotation of the disk (in radians per second). So for a short displacement the distance d = PP' is:

d ~ v. Dt² .W

That sideways distance d is traveled in time t, resulting from a sideways acceleration a, i.e.

d = a. Dt²/2 = v.W. Dt²

So the Coriolis acceleration is (1):

a = 2.v.W

The Earth' rotation rate around the local zenith is W_e sin l, where l is the latitude and W_e the Earth's rotation rate (2p/1 day)

Fig 1. Derivation of the Coriolis force.