The Reynolds', Richardson's, and Froude numbers

The behaviour of fluid flow depends on some simple criteria, and these criteria can be expressed as a dimensionless number or ratio. A ratio is a ‘pure’ number, like p, the ratio of the circumference to the diameter of a circle, where these distances are both measured in feet, metres or whatever.

Dimensionless numbers are attractive to atmosphere and ocean dynamics because they are scale-independent. For instance, the flow in a laboratory tank is similar to that in the atmosphere if certain ratios are the same. One obvious ratio distinguishes convective mixing from stratified conditions: convection occurs when the ratio of the actual to the adiabatic lapse rate exceeds one (Section 7.3). Several other criteria exist that separate between flow patterns, and they have been named after the people who discovered their meaning.

Static instability in the atmosphere leads to spontaneous vertical mixing (convection) in the form of thermals and possibly cumulus clouds (Section 7.4). Vertical mixing may occur in a stable environment, in particular in the form of breaking waves. These breaking waves are a major cause of turbulence aloft, especially just above the planetary boundary layer or near the jet stream, where they often produce clear-air turbulence (CAT) dreaded by aviators. The evolution of these breaking waves has been described mathematically by Kelvin and Helmholtz, hence the term Kelvin-Helmholtz billows, the evolution of which is shown in Fig 1. The likelihood of Kelvin-Helmholtz instability can be evaluated by means of the Richardson's number (Ri), the ratio of the static stability (N²) to the square of the wind shear (dU/dz):

Here U is the wind speed, g the gravitational acceleration (about 9.8 m/s²), q the potential temperature, and z height. N the Brunt-Vaisalla frequency, or static stability parameter: the higher N, the more stable the flow. Both stability and wind shear are calculated locally, and Ri may vary rapidly across a sheared boundary, such as on top of the stable nocturnal boundary layer. Even under these statically stable conditions, instability is possible, when the wind shear is strong enough to break up the stable layer and produce breaking waves. This occurs when Ri < 0.25 (1).

Fig 1. Idealized evolution of a Kelvin-Helmholtz billow when Ri < 0.25 .

Instability of airflow may be expressed in terms of the Reynolds’ Number (Re), which is the ratio of inertial and viscous forces.

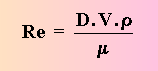
Here, D is the characteristic flow depth, V the wind speed, r the air density, and m the kinematic viscosity. The ratio Re is proportional to the wind speed; viscous forces dominate at low speeds, so that Re is small, whilst inertia is great at high speeds, making Re large. It is observed that fluid flow becomes turbulent when Re exceeds about 1400. This can be seen in cigarette smoke, which accelerates upwards from the burning tip, eventually reaching a speed at which the rising filament breaks into turbulence. Re is important in aeronautical sciences (the airflow around a wing) and in a variety of engineering applications. For instance, an oil pipeline needs to be designed so that Re>1, otherwise frictional retardation gains the upper hand. The viscosity increases as temperature decreases. Therefore in Alaska, a large pipe diameter is required, and the oil is heated.

The speed of shallow water waves c= sqrt(gh), where h is the depth of the flow, or, equivalently, the amplitude of the waves (i.e. the height of the obstacle H that triggered the waves). In the case of surface waves, the restoring force is the gravity g, but for waves internal to the atmosphere, the restoring force is the reduced gravity g'

(The prime ' refers to a small perturbation.) Therefore c= N.H, and the Fr can be expressed as

where H is the height of the mountain. If Fr<<1, i.e. when the airflow is slow, stably stratified, and/or the mountain high, the air will flow around the mountain, not over (if the mountain is too wide, the flow will be blocked). If however Fr>>1, the air readily flows over the mountain with very little lateral displacement. This leads to orographic rainfall or, if the air is drier, sometimes spectacular lenticular clouds.

Imagine airflow crossing a long mountain range whose width W (base-to-base) equals p.H. Then, for Fr = 1, the oscillation frequency triggered by the flow over the range, 2.p.U/(2W), equals the air's natural oscillation frequency N, i.e. 2.p.U/(2W) = U/H = N. In this case, there is considerable descent of air on the lee side, since the natural wave motion fits the shape of the mountain, and a series of mountain waves may be found downstream of the range (2). The more stable the air, the higher its natural oscillation frequency. And the higher the wind speed and the smaller the mountain obstacles, the higher the triggering frequency will be. A harmonic oscillation results if the two frequencies match. This may further be amplified if a sequence of mountain ranges exists, each spaced one or an integer multiple (m) of 'natural' wavelengths (m.U/N). This sometimes happens over the Basin and Range country of Nevada.

In a neutrally stable atmosphere, the Brunt-Vaisalla frequency N=0 and Fr becomes infinitely large. In this case the air readily flows over even isolated hills. In such a situation the wind accelerates slightly, to compensate for the thinned flow channel (air mass continuity). Tower measurements on a hill in Canberra 170 m high and 550 m wide indicate that the wind speed is up to 7% higher than upwind. The maximum velocity was reached at a height of 34 m above the crest (3). In the rare situation of an unstable atmosphere, the air will spontaneously rise over the mountain, possibly leading to thunderstorms.

The Scorer Parameter (L) is a related pure number, given by the following (2) -

L² = D² - (1/U) (d²U/dz²)

where D = N/U and (d²U/dz²) is the second derivative of the change of wind speed with height. The Scorer Parameter gives the wavelength l of any train of vertical motions (and lenticular clouds) downwind of a mountain range athwart the wind, as follows -

l = 2.p/L

Such a train forms if the L is a maximum at the height of the barrier.

1. Chapman, D. and Browning, K. A., 1997. Radar observations of wind-shear splitting within evolving atmospheric Kelvin-Helmholtz billows. Quart. J. Roy. Meteor. Soc., 123, 1433-1439.
2. Sturman, A. and N. Tapper 1996. The Weather and Climate of Australia and New Zealand. (Oxford University Press) 476pp.
3. Bradley, E.F. 1980. An experimental study of the profiles of wind speed, shearing stress and turbulence at the crest of a large hill. Quart. J. Roy. Meteor. Soc., 106, 101-23.